Humanidad vs Inteligencia Artifical - El juego de Go
Hace unos días ocurrió un evento que sorprendió a la comunidad de inteligencia artificial en todo el mundo. Investigadores en DeepMind (una compañía de Inteligencia Artificial que le pertenece a Google) desarrollaron software que tras ser entrenado, logró vencer a el campeón del juego de mesa Go, llamado Sedol Lee. El duelo fue de 5 juegos, donde la puntuación final fue de 4 a 1, a favor de la máquina.
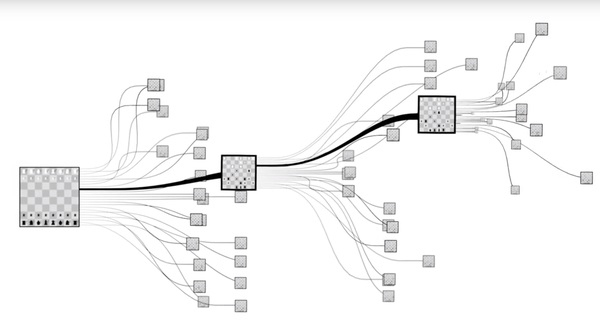
El nombre de esta AI es AlphaGo, y si nunca has jugado Go, o no estás enterado de los grandes retos de la inteligencia artificial, podría parecerte cosa simple (recordemos que en 1997 Garry Kasparov fue derrotado por DeepBlue); pero que un sistema computacional logre vencer a un campeón humano en Go es cosa muy seria. El juego de Go es computacionalmente mucho más complejo que el Ajedrez. Esto es así porque cada turno en un juego de Go tiene unas 200 posibilidades distintas, mientras que en un juego de Ajedrez sólo son unas 20 posibilidades cada turno - esto significa que el juego de Go tiene muchísimos juegos posibles - muchos más que el ajedrez - checa la Figura 1.
 </img>
</img>
 </img>
</img>
Figura 1. Figuras mostrando el factor de ramificación, o branching factor del Ajedrez (arriba) y el Go (abajo). Aquí es posible apreciar que el espacio de búsqueda de Go es enorme.
De hecho, ningún sistema computacional anterior a AlphaGo había logrado jugar al nivel de un jugador profesional de Go. Más aún, a diferencia de DeepBlue, que es un sistema con reglas y puntuaciones diseñadas por humanos; AlphaGo es un sistema que ‘aprendió’ a jugar tras ser expuesto a muchos juegos de Go. Este aprendizaje fue a través de redes neuronales profundas, una tecnología que sigue rompiendo las barreras de la inteligencia artificial. Por eso es que la noticia es tan importante.
Pero antes de meternos a hablar de AlphaGo y de Deep Learning, demos un paso atrás. De hecho, DeepMind y Google no son los primeros en utilizar redes neuronales para resolver problemas complejos como éste. Aproximadamente desde 2012, las redes neuronales profundas han sido utilizadas para resolver problemas que hasta antes parecían ser demasiado complejos y requerir demasiada inteligencia.
Sin duda, el término red neuronal suena interesante, pero en realidad ¿qué es una red neuronal?
¿Qué son las redes neuronales y quién las inventó?
En realidad, el nombre completo es ‘red neuronal artificial’. Es una estrategia para procesar información que fue inspirada por la manera en que funciona el sistema nervioso de organismos vivos. Normalmente son utilizadas para estimar funciones que pueden depender de varios parámetros, y en general son desconocidas y no-lineales. Tal vez recuerden cómo en un post anterior codificamos un perceptron: Una neurona básica, utilizada en esquemas de clasificación.
Los primeros intentos para diseñar y utilizar redes neuronales artificiales fueron en los 40s. Warren McCulloch, y Walter Pitts desarrollaron el primer modelo en 1943, y de ahí nació la investigación en redes neuronales. El campó siguió creciendo en los 50s y 60s.
En 1969, el profesor Marvin Minsky, de MIT publicó el libro ‘Perceptrons’, donde estudia a detalle, y estrictamente las redes neuronales artificiales con Perceptrones. Entre otras cosas, Minsky concluyó que el modelo de redes neuronales no se beneficiaría mucho de volverse más complejas. Al día de hoy, se le da crédito a este libro por provocar que se perdiera interés por las redes neuronales a lo largo de la década de los 70s. De hecho, en este periodo, y hasta finales de los 80s hubo muy pocos investigadores realizando investigación, pero estos pocos investigadores fueron poco a poco avanzando el campo de las redes neuronales.
Todo cambió en 2012 en el concurso de ImageNet, que es un concurso donde investigadores proponen algoritmos inteligentes para buscar objectos dentro de imágenes. Alex Krizhevsky de la Universidad de Toronto utilizó una red neuronal profunda, y logró arrasar con todos los records establecidos hasta ese momento.
Exactamente ¿Cómo funciona una red neuronal?
Una red neuronal artificial es un sistema de varias ‘neuronas’ interconectadas. Una neurona artificial es un elemento con varias entradas y una salida. Una neurona puede operar en dos modos: Modo de entrenamiento, y modo de ‘uso’, o de predicción.
 </img>
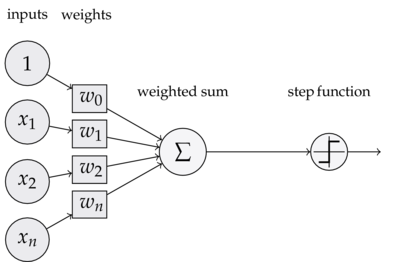
</img>Figura 2. Una neurona simple con 3 entradas ponderadas (observa los parámetros w) y una salida.
Cuando la neurona de la Figura 2 está en modo de predicción, la salida está dada por el promedio ponderado de las entradas, y el término independiente, como se puede ver en la Figura 3.
 </img>
</img>Figura 3. Ecuación de la salida del perceptrón.
Sin embargo, la parte más interesante de una red neuronal es su entrenamiento. Ya vimos en el post del Perceptron cómo se entrena un Perceptron básico. Para entrenar redes neuronales con más de una capa se utiliza un algoritmo llamado Retropropagación de errores, o en inglés “Backpropagation”.
 </img>
</img>Figura 4. Una red neuronal con una capa oculta.
Retropropagación
El algoritmo de retropropagación de errores tiene dos fases básicas:
1. Fase de Propagación
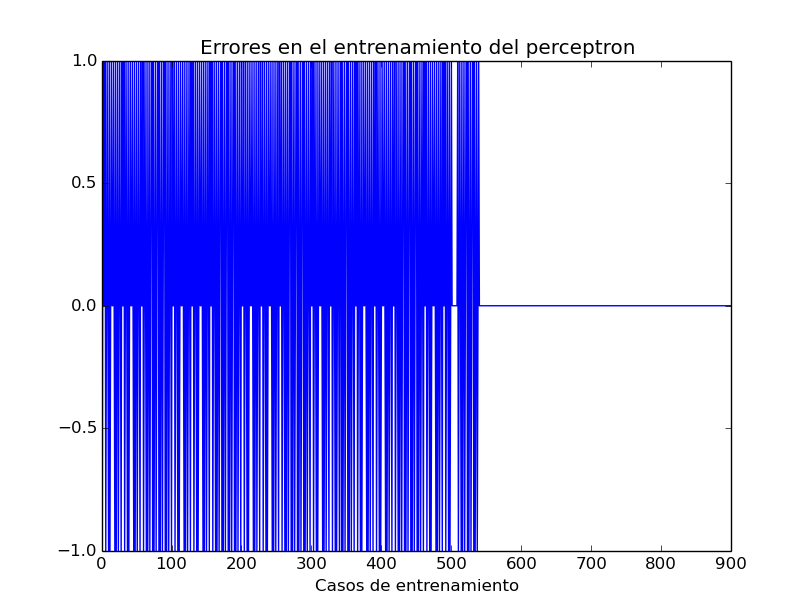
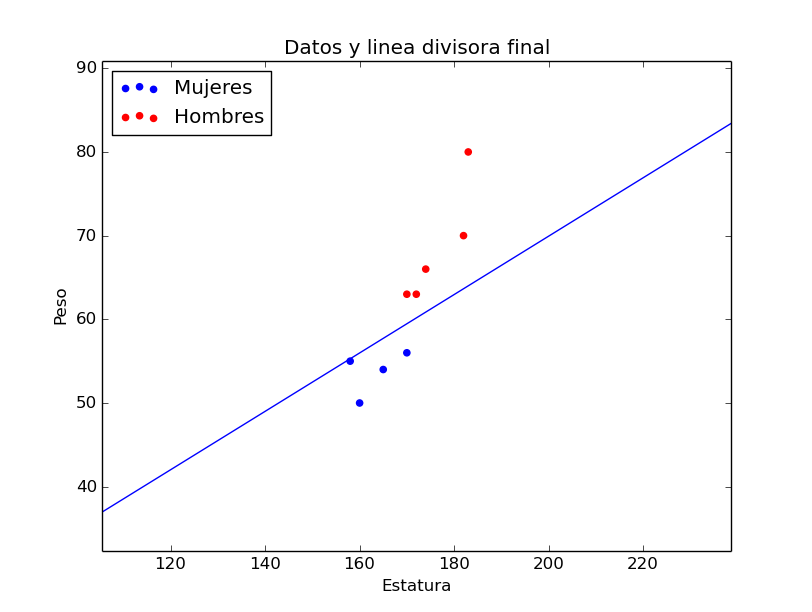
Propagación de un patrón de entrenamiento a través de la red. Es decir que dado el estado de la red, un ejemplo de datos X (por ejemplo la estatura y el peso de una persona), y una salida esperada (por ejemplo, si la persona es hombre o mujer), introducimos X a la red, y observamos la salida calculada por la red.
Si la salida de la red es diferente de la salida Y, entonces realizamos retropropagación de los errores encontrados en cada capa de la red, para obtener las deltas: la diferencia entre la salida observada y la salida correcta.
2. Fase de Actualización de las Ponderaciones
Multiplicar la delta de salida y la activación de entrada para obtener el vector gradiente de las ponderaciones, y substraer una fracción del vector gradiente de las ponderaciones. Eso básicamente significa que vamos a obtener el error, y empujar las ponderaciones un poquito para reducir el error.
Para imaginar este proceso un poco mejor puedes checar esta visualización del algoritmo de retropropagación, donde puedes ver cómo los pesos de una red neuronal son ajustados poco a poco hasta converger. Como ven, los pesos en la capa más lejana a la salida son ajustados muy lentamente. Ahora imagina 20 capas más!
En un post posterior vamos a ver un ejemplo del algoritmo de retropropagación aplicado a un problema de clasificación.
¿Y qué es deep learning?
En 1989, Yann LeCun demostró el primer sistema de redes neuronales profundas que utilizaba el algoritmo de retropropagación, y constaba de 5 capas. La red de LeCun (quien ahora trabaja para Facebook) fue utilizada para reconocer códigos postales escritos a mano en sobres postales. La red tomó tres días para ser entrenada, y resultó ser muy efectiva.
Como lo mencionamos en la sección de retropropagación, uno de los principale problemas al entrenar redes neuronales profundas es el tiempo que tardan en converger hacia soluciones. Sepp Hochreiter fue el primer investigador en estudiar este problema de manera analítica. Así encontró el Vanishing Gradient Problem, o ‘problema del gradiente que se desvanece’ (perdonen la mala traducción). Este problema ocurre porque, como vimos en el algoritmo de retropropagación, entre más profunda sea la red, más lento es lograr que las ponderaciones de las entradas en la red lleguen a la solución. De hecho, AlphaGo utilizó 50 GPUs para su fase de entrenamiento.
AlphaGo
El programa AlphaGo no es puramente una red neuronal profunda. De hecho, AphaGo funciona con un algoritmo de búsqueda Monte Carlo, que es la técnica clásica para Inteligencias Artificiales en juegos por turnos. La diferencia es que a la hora de seleccionar los mejores movimientos, en vez de utilizar reglas y heurísticas preprogramadas (que es lo que se había utilizado hasta ahora), AlphaGo utilizó un conjunto de dos redes neuronales profundas que fueron entrenadas incialmente con millones de juegos de expertos y amateurs de Go; y posteriormente, AlphaGo entrenó jugando contra sí mismo.
La red neuronal más importante en AlphaGo es conocida como policy network, o una red de “reglas”. Lo interesante es que este tipo de red es muy utilizada en análisis de imágenes - y el tablero de Go también es analizado omo si fuera una imagen de 19x19 pixeles!
El resultado fue una inteligencia que es bastante buena para localizar los mejores movimientos en un juego… Pero que además requiere de mucho procesamiento paralelo para realizar el algoritmo de búsqueda Monte Carlo: 1,202 CPUs y 176 GPUs. Si quieres saber más al respecto, checa el artículo de DeepMind en la revista Nature.
Las redes neuronales hoy en día
Y esa es la historia de las redes neuronales. En la actualidad, casi cada semana hay una noticia emocionante que tiene que ver con ellas. Por ejemplo, cuando Google abrió el código de su herramienta interna TensorFlow, o que algunos rockstars de la inteligencia artificial iniciaron la fundación OpenAI, o cuando DeepMind consiguió que su algoritmo aprendiera a jugar videojuegos mejor que jugadores humanos. Hay montones de aplicaciones donde las redes neuronales han resultado ser muy útiles, como reconocimiento de imágenes, procesamiento de lenguaje natural y sistemas de recomendación; sin embargo, aún existen muchos desafíos para el avance de esta tecnología.
Uno de los desafíos más interesantes viene del costo computacional que es construir redes neuronales profundas, que requieren muchos datos. De hecho, conforme las redes se vuelven más amplias y más profundas, el tiempo que toma crearlas y entrenarlas con datos aumenta mucho. Esto ha llevado a que el software sea optimizado muchísimo, al grado que existen muchas librerías que permiten utilizar tarjetas gráficas (GPUs) para entrenar las redes neuronales (e.g. TensorFlow, Caffe); sin embargo, poco a poco se vuelve evidente que existirán aplicaciones que requieran hardware especializado. Por esto es que IBM creó TrueNorth, un procesador diseñado como una red neuronal, para ejecutar y entrenar redes personalizadas. Sin embargo, el problema de hardware de las redes neuronales aún no está resuelto. Queda mucho espacio para explorar.
Otro desafío importante es el de toma de decisiones de largo plazo. Las redes neuronales actuales aún no han alcanzado inteligencia que les permita planear y tomar decisiones con resultados de largo plazo. Hay mucha investigación en este aspecto.
Finalmente, me gustaría señalar que la historia es excelente, pero no olvidemos que AlphaGo no es sólo una red neuronal: es un sistema muy complejot de 1,200 CPUs y casi 180 GPUs - Enfrentando a un chico de 30 años de edad, que incluso consiguió vencer a AlphaGo una vez.
En fin, espero que el post fuera informativo - y gracias por la paciencia ; ). Comentarios bienvenidos.

 </img>
</img>
 </img>
</img>
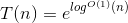 . Esta función no es exactamente polinomial, así que se le llama cuasi-polinomial.
. Esta función no es exactamente polinomial, así que se le llama cuasi-polinomial.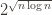 . Como ven, este viejo algoritmo tiene un factor polinomial dentro del exponente, así que es un algoritmo cuasi-exponencial. Es decir que la diferencia es muy grande.
. Como ven, este viejo algoritmo tiene un factor polinomial dentro del exponente, así que es un algoritmo cuasi-exponencial. Es decir que la diferencia es muy grande. Figura 1. Una red o grafo simple con cuatro nodos.
Figura 1. Una red o grafo simple con cuatro nodos. </img>
Figura 2. Árbol de probabilidades en una caminata aleatoria.
</img>
Figura 2. Árbol de probabilidades en una caminata aleatoria.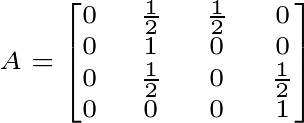 </img>
Figura 3. Matriz del Proceso de Markov para la caminata aleatoria en el grafo de la Figura 1.
</img>
Figura 3. Matriz del Proceso de Markov para la caminata aleatoria en el grafo de la Figura 1.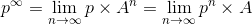 </img>
Figura 4. Ecuación de la distribución estacionaria.
</img>
Figura 4. Ecuación de la distribución estacionaria.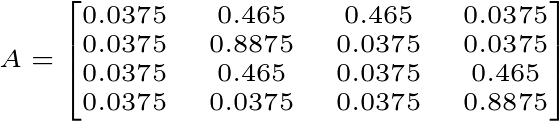 </img>
Figura 5. Matriz completa de pagerank para el grafo de la Figura 1.
</img>
Figura 5. Matriz completa de pagerank para el grafo de la Figura 1.